Learn the tricks and tips for solving any Sudoku puzzle with ease. Get the facts on understanding solving Sudoku strategies and becoming a master of this classic game.
Unveiling the Solving Sudoku Strategies
Do you enjoy the challenge of solving a Sudoku puzzle? Or do you find yourself frustrated and overwhelmed by seemingly endless rows of numbers? Either way, this blog post is here to help.
We’ll go over some useful solving Sudoku strategies that will make your journey into solving these tricky puzzles easier and more enjoyable!
With just a few specific techniques, you’ll be able to approach every task with confidence and ease. So don’t let those overwhelming grids scare you anymore – come join us as we explore the exciting world of Sudoku puzzles!
Introduction to Sudoku
Developed in 1979 by American Howard Garns, this challenging game of logic and trial-and-error has gained widespread popularity since 2005. But Sudoku is more than just a game – it involves fascinating mathematical concepts like combinatorics, group theory, and computational complexity.
The journey of Sudoku began when Japanese inventor Maki Kaji published it in his puzzle company’s magazine in 1984. Renaming it to Sudoku, meaning “Single Numbers”, Kaji set off a frenzy in Japan. Soon, New Zealander Wayne Gould caught onto the Sudoku craze and brought it to the attention of the world by having puzzles printed in The Times newspaper in London. England caught Sudoku fever, and by 2005, the U.S. finally embraced this addictive puzzle game.
So, what exactly is Sudoku? It’s a 9×9 grid containing 81 cells, divided into nine 3×3 blocks. Some cells are already filled in with numbers, known as givens. The goal is to fill in the empty cells with the numbers 1 to 9, ensuring that each row, column, and block contains every number exactly once. This rule, known as the One Rule, creates a satisfying challenge that keeps enthusiasts coming back for more.
But Sudoku doesn’t stop there. It comes in different levels of difficulty and sizes, with grids as large as 16×16. No matter the rank, the objective remains the same – solve the puzzle by applying logic and reasoning to achieve a complete grid.
Join the millions of Sudoku enthusiasts around the world and embark on this captivating puzzle journey. Challenge your mind, immerse yourself in the world of math, and become a Sudoku master today.
Rules of Sudoku Game
Sudoku is a challenging yet enjoyable puzzle that requires logical thinking and attention to detail. In this blog post, we will explore the three essential rules of Sudoku and provide you with valuable insights to help you become a master Sudoku solver.
Rule #1: Each row holds the numbers 1-9 exactly once:
Visualize the Sudoku grid as a 9×9 layout with rows running from left to right. Your goal is to place the numbers 1-9 into each row’s empty cells, ensuring that no number is repeated.
Rule #2: Each column houses the numbers 1-9 exactly once:
Similar to rows, the columns play a crucial role. Fill each column with the numbers 1-9, making sure that no duplicates exist.
Rule #3: Each 3×3 box encompasses the numbers 1-9 exactly once:
Focus on the smaller 3×3 subregions, known as “boxes.” Each box must contain the numbers 1-9 without repeating any number. By mastering these three rules, you’ll guarantee a unique solution for every row, column, and box.
By embracing these three vital rules, you’ll experience the satisfaction of solving Sudoku puzzles effortlessly. No need to worry about diagonal lines, as the two 9-cell diagonals do not require the numbers 1-9 to be present. With logical thinking and attention to detail, you’ll successfully solve any Sudoku puzzle and enjoy the sense of accomplishment that comes with completing it.
Discover the Best Solving Sudoku Strategies for You
Sudoku enthusiasts employ various strategies to conquer puzzles, but the effectiveness of each method varies greatly depending on who you ask. Ultimately, the key to success in Sudoku lies in finding the strategy that resonates with you the most.
If one approach fails, don’t despair. There are plenty of alternatives to explore. You can either try a different strategy or even combine multiple strategies to crack the puzzle.
As you delve deeper into this guide, you will come across commonly used strategies that have proven helpful for countless puzzle solvers.
While some strategies require advanced skills, others are beginner-friendly. Remember, the most important factor is finding what works best for your logical reasoning.
Avoid getting fixated on a single strategy. It’s perfectly alright to have a preferred approach, but remember that sometimes you may need to switch to a different strategy to overcome challenges.
If you find yourself stuck, don’t hesitate to revisit the other strategies discussed here. One of them is sure to provide the breakthrough you need.
The Naked Pairs Strategy involves analyzing a Sudoku puzzle to determine the only possible numbers that can fit in a particular cell. This strategy is similar to the process of elimination used at the beginning of a puzzle.
When encountering a naked pair, two possible numbers can be used, but it is unclear which number goes where.
By identifying a naked pair, you can eliminate the option of using those numbers in any other row, column, or square. It then becomes a matter of deduction to determine which number makes the most sense based on the surrounding row or column.
For example, if a naked pair consists of either a two or a six, you must check to see where those numbers are already used in the puzzle, bearing in mind that no digit can be repeated.
It is important to note that naked pairs do not need to align within the Sudoku grid. They can be scattered within the square as well.
The key to this strategy is understanding that there are only two possible numbers for the cells in question, and using the process of elimination to identify the correct one.
Additionally, the same concept can be extended to naked triplets or quads, which are more challenging because they involve solving a larger portion of the puzzle compared to naked pairs.
Overall, the Naked Pairs Strategy is a powerful technique that can help advanced Sudoku players make progress in solving complex puzzles.
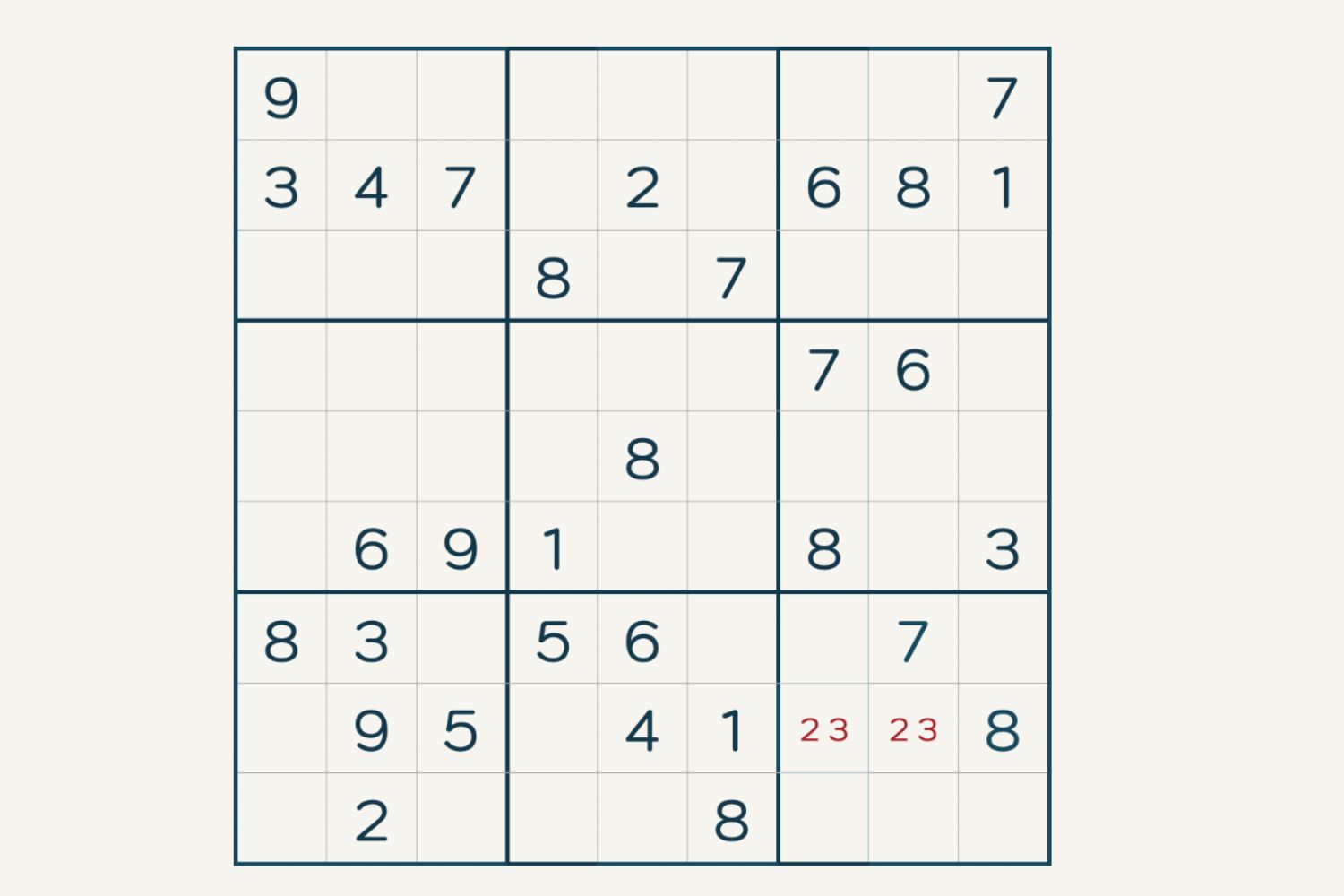
Hidden Pairs Strategy
Discover the ultimate technique to uncover hidden patterns and strategically place numbers in your Sudoku grid. The hidden pair strategy allows you to eliminate clusters of numbers from two cells, simplifying your options for the remaining cells. It serves as a foundational strategy for more advanced gameplay.
To implement this strategy, first examine the filled-in numbers in your Sudoku grid. Then meticulously scan the columns, rows, and squares to rule out those numbers as potential options. By doing so, you will reveal a straightforward pair of number options that you can use to dominate the game.
In the example above, the hidden pair may initially appear overwhelming with various number possibilities. However, by diligently following the rule of scrutinizing columns and rows, you’ll unveil that the true value of those cells can only be 6 or 7. Through the hidden pairs strategy, you have successfully eliminated all other options.
While this strategy can also be applied to triplets or quads, mastering them may require more practice. It is advisable to begin honing your skills with pairs and gradually progress to more complex scenarios.
Open up your Sudoku grid to new possibilities and unleash the hidden pairs strategy to dominate the game.
Pointing Pairs Strategy
The Pointing Pairs Strategy is a technique used in solving grids. It involves identifying a number that consistently appears as a possibility within a specific square.
When these numbers are aligned in the same column or row, they form a pointing pair. This pointing pair indicates that the number must be used in that line and can be excluded from other cells.
Put simply, when a repeated possibility is aligned within a square, it “points” to where in the rest of the row or column the number can be eliminated.
For example, if you notice that the number 3 is a recurring possibility and it is aligned in the same row or column within the square, you can confidently remove 3 as a possibility from any other cell in those rows or columns.
It is important to note that the number 3 must be placed within the square you are looking at; the challenge lies in determining which of the two cells the 3 will be used in.
This strategic approach allows you to rule out numerous possibilities and enables you to fill in some rows or columns, as you already know that a 3 cannot go in any of those cells.
Overall, the pointing pairs strategy provides a structured method for systematically searching and eliminating possibilities, rather than relying on random deductions.
Intersection Removal Strategy
The Intersection Removal Strategy is an effective method for solving puzzles by eliminating possibilities. By focusing on ruling out numbers that cannot go in certain places, rather than trying to determine the correct placement, this strategy simplifies the puzzle-solving process.
To apply this strategy, look for any number that appears as a possibility two or three times within a single unit (row, square, or column).
Once identified, you can then remove that number from any intersecting units. It is important to fully understand what constitutes a unit in the game, as the goal is to solve the entire grid, not just individual squares.
When a pair or triplet of numbers intersects with another row, column, or square, you can eliminate them as possibilities for that intersecting unit.
This systematic process of elimination brings you closer to the final result. While it requires a bit more focus on the entire grid, the Intersection Removal Strategy is a valuable tool for puzzle-solving.
X-Wing Strategy
When it comes to Sudoku, the X-Wing Strategy is a game-changer. Instead of fixating on individual squares, this strategy focuses on parallel rows and columns, allowing you to eliminate possible numbers and clear your board of those pesky pencil marks.
Forget about focusing on individual squares and embrace a new perspective. The X-Wing Strategy is all about parallel rows and columns. By identifying pencil marks that appear in the same two spots in two different rows, you can create an X formation that holds the key to solving the puzzle.
Take a look at the example provided. The parallel rows generate an X shape, which inspired the name of this game-changing strategy. Now you can see that each row in the X formation must contain a 4. The dark blue and light blue slots are the only valid options, as placing the 4 anywhere else would violate the rules of Sudoku.
But the X-Wing Strategy doesn’t stop there. Once you establish your X formation, take a step back and evaluate the entire grid. Look for any instances of repeated numbers, as they will guide you in making the right moves. Erase the unwanted numbers and confidently place the X formation numeral in its rightful cell.
Mastering the X-Wing Strategy requires patience and practice, but the results speak for themselves. This technique is not for the faint of heart, but if you’re ready to level up your Sudoku skills, it’s a game-changer.
Say goodbye to fixating on individual squares and rows/columns and hello to a broader perspective. Embrace the bigger picture and conquer Sudoku like a true pro.
Swordfish Strategy
Discovering the next level of Sudoku mastery, the Swordfish Strategy takes the concept of the X wing to a whole new level. Instead of just two rows and two possible numbers, this advanced strategy challenges solvers to find three possible numbers in three rows or columns.
While not for the faint of heart, the Swordfish Strategy is far from useless. It may be perplexing to spot at first, but the potential for success is undeniable.
By carefully examining the image, pay attention to the red lines that indicate the possibility of a 5 in the corresponding slots of the red-lined rows.
Dive deeper into the strategy with the blue lines that reveal where a 5 aligns and crosses the line. These intersections highlight the potential placement of a five. Conversely, if there is no intersection between a blue and red line, you can confidently eliminate five as a candidate for that cell.
Remember, the purpose of blue lines is not to pinpoint the exact cell for the five, but to guide the elimination process. In the image, the blue-highlighted cells represent those that might contain a five, while the red-highlighted cells are definitively devoid of that possibility.
Approach the Swordfish Strategy with caution, as it requires heightened expertise in Sudoku solving and a deep understanding of grid patterns.
Novices may find it challenging to identify the patterns necessary for success and may struggle to complete their puzzle. This advanced technique is best suited for seasoned Sudoku enthusiasts who have honed their skills over time.
“Slicing and Slotting” for Sudoku Success
When you’re facing a Sudoku puzzle that stumps you, “slicing and slotting” is the technique you need. This powerful strategy helps you break down the puzzle into manageable rows of three, enabling you to analyze missing or incorrect numbers with precision.
Here’s how it works: Start by dividing the puzzle into rows of three and carefully analyze each row. Compare the numbers in a numeric order, looking for any blank spots. Take note of the possibilities for each blank spot by considering the pencil marks you made earlier. This technique works particularly well if you have already eliminated some candidates.
While examining the three rows, pay attention to where there are already cells with the number you’re scanning for. For example, if you’re looking for the number 1, take note of its location in the three rows. Then, observe how the number interacts with the unsolved cells.
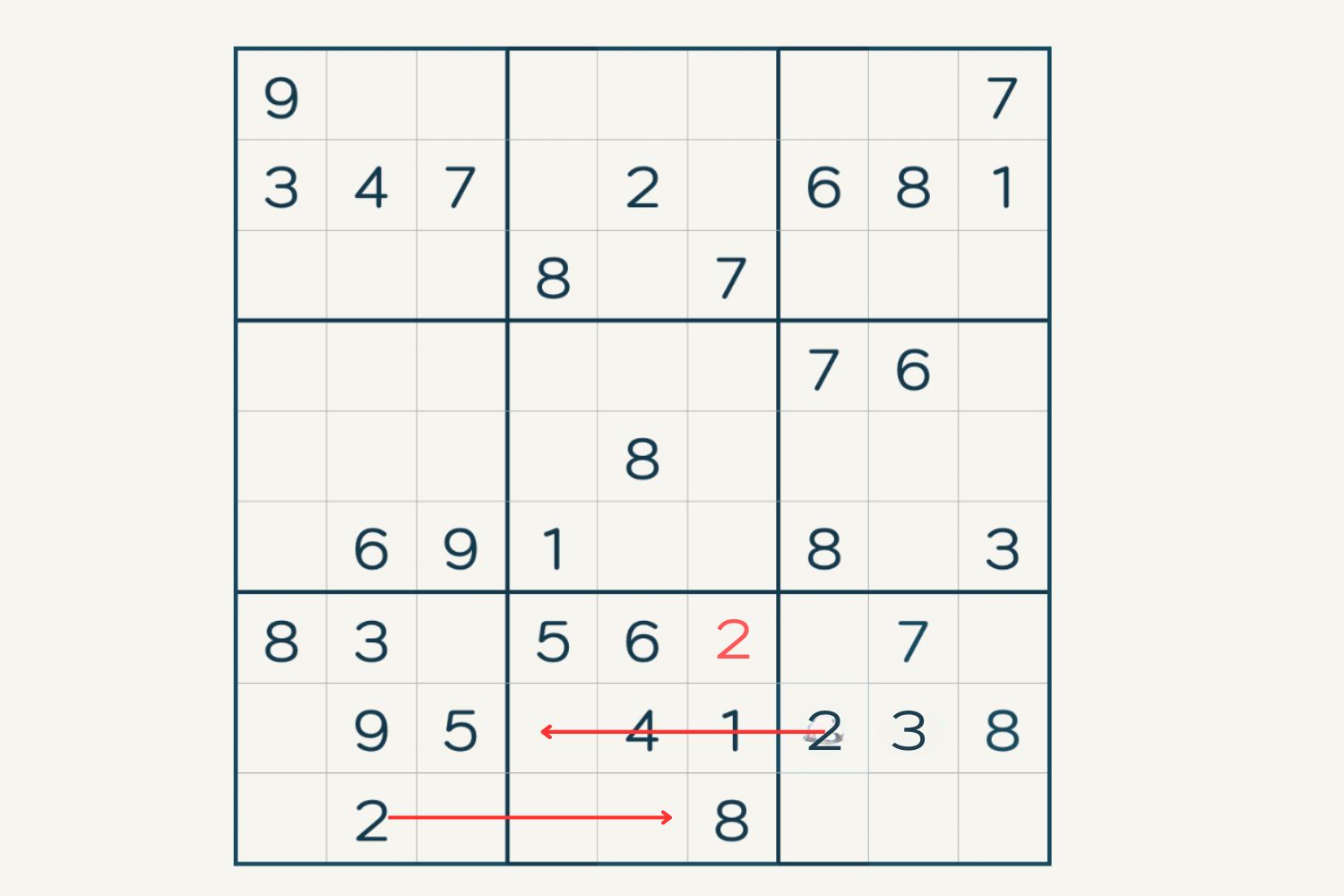
Let’s say you’re scanning for the number 1 and find it within one of the rows. Check the candidates in that particular square, row, and column. If you see 1 as a candidate in any of those areas, you can eliminate it as a possibility. Since the number is already present in the row, column, or square, it cannot be placed there.
To see this concept in action, refer to the image above. Notice the red lines, which indicate that a 2 cannot be placed in any position where there’s a red line. Once the 2 has been used in a row, square, or column, it cannot be reused. Thus, if you had a 2 as a candidate in any of the areas marked with a red line, you could eliminate it.
Remember, slicing and slotting are not guaranteed to solve your Sudoku puzzle, but they can provide a helpful breakdown and a fresh perspective. Sometimes, all you need is a microfocus to see what’s going on. Try incorporating this technique into your Sudoku-solving process and see the difference it makes.
FAQs
Is Mathematics the Key to Solving Sudoku Puzzles?
When it comes to solving Sudoku, the concept of “math” can be misleading. Many people wonder about the numbers that need to be added up to solve the puzzle. However, Sudoku puzzles do not involve arithmetic operations like addition or subtraction.
In reality, Sudoku is a game that revolves around symbols, with numbers being the most widely recognized version.
But you could easily use shapes or other symbols and still have the same type of puzzle with the same rules and outcome. Some Sudoku variants use letters or symbols instead of numbers to add variety.
That being said, Sudoku does require mathematically logical thinking. So, if you’re asking whether math plays a role in solving these puzzles, the answer is yes.
However, it’s not the traditional math you might be thinking of. Sudoku is solved through logical reasoning that heavily relies on mathematical concepts.
Discover the intriguing world of Sudoku, where mathematics meets logic. Challenge your mind and unlock the secrets of this captivating puzzle game.
Is It Possible for a Sudoku Puzzle to Be Unsolvable?
Although there may be differing opinions within the Sudoku fan community, it is generally agreed upon that a genuine Sudoku puzzle is always solvable.
It is said that a legitimate Sudoku puzzle has only one unique solution. If you encounter a puzzle that cannot be solved, it is likely due to a printing error or it is not a true Sudoku puzzle, but rather a variation based on the Sudoku grid.
Some specific websites and publications purposely create unsolvable puzzles, but this is done intentionally. These puzzles are meant to provide a fun challenge for avid Sudoku fans.
The appeal of attempting to solve something that has been claimed to be unsolvable is a major attraction for these types of platforms.
What Should I Do If I’m Stuck On A Sudoku Puzzle?
If you find yourself stuck, one option is to start fresh. Clear the board and give yourself a clean slate. Alternatively, for a greater challenge, you could try erasing rows or columns with repeated numbers. However, be cautious as this might only lead to more frustration.
When starting over, explore new strategies that you haven’t tried yet. This fresh perspective might be the key to solving the puzzle successfully.
Remember, not every puzzle is solved by every person, but every puzzle does have a solution. Sudoku is a game that requires skill development, so don’t get discouraged if you have to start anew. It’s all part of the learning process.
Continue experimenting with the strategies you’ve learned and find what works best for you. Even the most skilled Sudoku solvers don’t use every strategy available. The path to the solution is up to you, as long as you reach the single solution to the puzzle.
Keep in mind that Sudoku is meant to be a brain-teasing and enjoyable activity. Once you grasp the basics, you’ll be ready to take on higher difficulty levels and truly appreciate your time spent playing.
Conclusion
Sudoku puzzles can be a great way to challenge yourself and develop your problem-solving skills. Taking the time to understand different strategies for completing these complex puzzles can be an immensely rewarding experience.
With practice and patience, anyone can become a master at Sudoku! By building upon your newly found knowledge of solving strategies, you can take on more difficult challenges, explore new cognitive-based abilities, and create satisfying outcomes.
We urge you to give Sudoku puzzles a try and work through them strategically to become the most efficient solver possible. Not only will it keep your mind sharp but will also result in the ultimate satisfaction that comes with success!
Thanks for reading our article Solving Sudoku Strategies. If you want to know more information, visit our website here.
Read more: